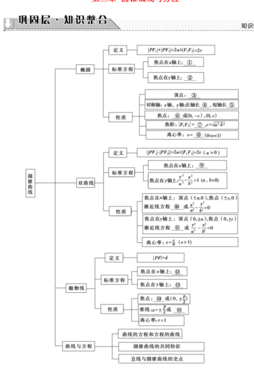
圆锥曲线方程
1、圆锥曲线的方程一般是:Ax+By+Cxy+Dx+Ey+F=0。其中A,B,C,D,E,F为实参量,且要求A,B,C不全为零。
2、圆锥曲线标准方程是轨迹的方程,也是参数方程的一种;圆锥曲线标准方程的定义和性质是把握圆锥曲线标准方程的两把钥匙。
3、圆锥面的曲面方程:z=根号下(X2+Y2)。通过一个定点V且与定曲线r(它不过定点V)相交的所有直线构成的曲面称为锥面;如果母线是和旋转轴斜交的直线,那么形成的旋转面叫做圆锥面,这时,母线和轴的交点叫做圆锥面的顶点。
高二数学圆锥曲线与方程
1、设直线与曲线相交两点坐标(x1,y1)(x2,y2),带入圆锥曲线方程,得出两个方程。
2、设直线PQ的t参数方程为x=a+tcosα,y=tsinα,(α为直线PQ的倾斜角,t为直线上的点到点M的距离。
3、这里只说下思路,若还有问题,再提:(1)由离心率可知a、c的关系,由短轴长可知b=1,再加上a方=b方+c方,可推得a=2 (2)由直线MD的方程和椭圆方程,可求得M点坐标,同理可求得N点坐标,可求得MN的长度。
4、高中数学合集百度网盘下载 链接:https://pan.baidu.com/s/1znmI8mJTas01m1m03zCRfQ?pwd=1234 提取码:1234 简介:高中数学优质资料下载,包括:试题试卷、课件、教材、视频、各大名师网校合集。
5、联立y=-(1/2)x+1和y=kx可得D点坐标(2/(2k+1),2k/(2k+1))设E(Xkx),F(x,kx) 易知E在第三象限,F在第一象限。
6、又知道b=所以解除一个范围。因为双曲线本身e>1。所以取交集。直接用向量方法做,对应系数相等。与y轴交点P是(0,1) 最后带入直线方程。得出两个点中的一个就够了。再代入双曲线方程。
圆锥曲线
圆锥曲线是指与圆锥截面相切的平曲线。圆锥曲线的一般方程式为:x^2/a^2 + y^2/b^2 = z^2/c^2 其中a,b,c为常数。
圆锥曲线常用的二级结论:椭圆∶焦半径∶a+ex(左焦点),a-ex(右焦点),x=a/c。双曲线∶焦半径∶|a+ex|(左焦点)|a-ex|(右焦点),准线x=a/c。
圆锥曲线的方程一般是:Ax+By+Cxy+Dx+Ey+F=0。其中A,B,C,D,E,F为实参量,且要求A,B,C不全为零。
圆锥曲线特点:从方程的形式来看:做直角坐标系中,这几种曲线的方程(包括圆)f(x,y)=0都是 二元二次 方程,所以统称二次曲线。
解析集合的角度,圆锥曲线统一定义:到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。当0e1时为椭圆:当e=1时为抛物线;当e1时为双曲线。