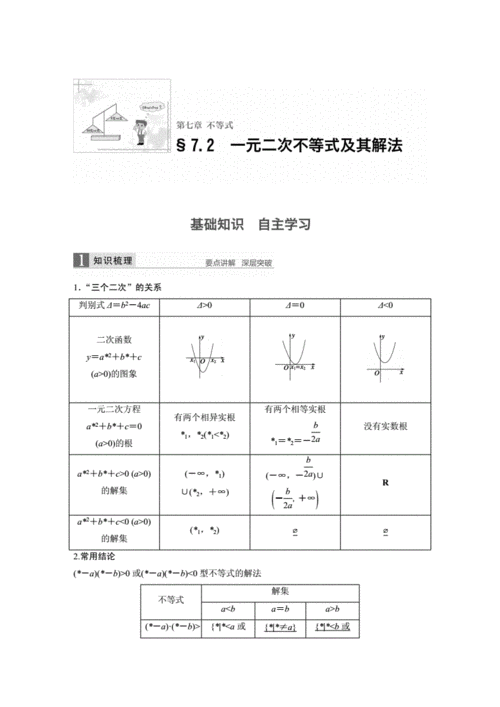
解一元二次不等式的口诀及步骤
1、这种方法叫做序轴穿根法,又叫“穿根法”。口诀是“从右到左,从上到下,奇穿偶不穿。”一元二次不等式也可通过一元二次函数图象进行求解。通过看图象可知,二次函数图象与X轴的两个交点,然后根据题中所需求0或0而推出答案。
2、首先化成一般式,构造函数第二站;判别式值若非负,曲线横轴有交点;a正开口它向上,大于零则取两边;代数式若小于零,解集交点数之间;方程若无实数根,口上大零解为全;小于零将没有解,开口向下正相反。
3、把x=7带入①,得7+y=9,解得y=2 ∴x=7,y=2 这种解法就是加减消元法。
4、解一元二次不等式口诀:首先化成一般式,构造函数第二站;判别式值若非负,曲线横轴有交点;a正开口它向上,大于零则取两边;代数式若小于零,解集交点数之间;方程若无实数根,口上大零解为全;小于零将没有解,开口向下正相反。
5、试解一元二次不等式 2x-7x+60 解:利用十字相乘法 2x -3 x -2 得(2x-3)(x-2)0 然后,分两种情况讨论 :口诀:大于取两边,小于取中间 1) 2x-30,x-20 得x5且x2。不成立 2)2x-30,x-20 得x5且x2。得最后不等式的解集为:5x2。
6、如果a0,就先变成2次项系数大于0的,把不等号方向改变下。
解一元二次不等式口诀?
1、一元二次不等式:含有一个未知数且未知数的最高次数为2的不等式叫做一元二次不等式。它的一般形式是ax^2+bx+c0或ax^2+bx+c0(a不等于0)其中ax^2+bx+c是实数域内的二次三项式。有两种判别方法:当a0时:判别式△(b-4ac)0时,有两个不相等的解。
2、举例:试解一元二次不等式 解:利用十字相乘法:2x -3 x -2 得(2x-3)(x-2)0 然后,分两种情况讨论。口诀同一元一次不等式的“数轴法”:大大取大,小小取小;大小小大取中间,小小大大没有解。
3、一元二次不等式先当做一元二次方程解出两个解,如果是大于号(大于0),则最右面的和最左面的两段为不等式的解,如果是小于号(小于0),则两个解中间的一段为不等式的解。
4、一元二次不等式的解法 1)当V(V表示判别是,下同)=b^2-4ac=0时,二次三项式,ax^2+bx+c有两个实根,那么ax^2+bx+c总可分解为a(x-x1)(x-x2)的形式。这样,解一元二次不等式就可归结为解两个一元一次不等式组。一元二次不等式的解集就是这两个一元一次不等式组的解集的并集。
一元二次不得式,我不懂,哪位老师可以给我详细讲解下!谢谢
二次三项式,ax+bx+c 有两个实根,那么 ax+bx+c 总可分解为a(x-x1)(x-x2)的形式。这样,解一元二次不等式就可归结为解两个一元一次不等式组。一元二次不等式的解集就是这两个一元一次不等式组的解集的交集。
首先应该明确,我们是要对a进行分类讨论,探讨a取不同值时,不等式的解集。在分类讨论的过程中,我们借着 抛物线形状决定解集这一理念,从入手。显然,此题为开口向上的抛物线,此时讨论 由此可见,我们讨论了a在整个定义域R上的全部情况,题目到此结束。
一正一负相乘小于零;另一种是X>0而X-1<0,理由同上。然后解这两个不等式组,就可得出X的取值范围是:(0,1)。你把解两个不等式组得出的X的取值范围在数轴上一画出,再对照结果,一看就会明白了。当然,都作完了以后,你也可以用X取一些数值,看解出的结果是否正确。
一元二次方程与不等式大于号和小于号的口诀
一元二次不等式先当做一元二次方程解出两个解,如果是大于号(大于0),则最右面的和最左面的两段为不等式的解,如果是小于号(小于0),则两个解中间的一段为不等式的解。
区分可以看符号的开口方向,开口向左为大于号,开口向右为小于号。不等式运算基本性质:如果xy,那么yx;如果yx,那么xy;(对称性)。如果xy,yz;那么xz;(传递性)。如果xy,而z为任意实数或整式,那么x+zy+z;(加法原则,或叫同向不等式可加性)。
以下是3个区别大于号和小于号的方法;大于号和小于号区分口诀:左边大,大于号;左边小,小于号。大于号开口在左边,小于号开口在右边。开口旁边是大数,尖尖旁边是小数。开口朝大数,尖尖朝小数。大于号是数学中不等式运算符号的一种。大于号被广泛运用在算数中,是小学必学的内容。