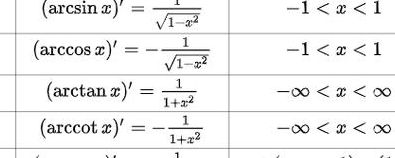反三角函数如何求导
1、反函数的导数等于直接函数导数的倒数 arccotx=y,即x=coty,左右求导数则有 1=-y*cscy 故y=-1/cscy=-1/(1+coty)=-1/(1+x)。
2、反正弦函数的求导:(arcsinx)=1/√(1-x^2)反余弦函数的求导:(arccosx)=-1/√(1-x^2)反正切函数的求导:(arctanx)=1/(1+x^2)反余切函数的求导:(arccotx)=-1/(1+x^2)三角函数是数学中属于初等函数中的超越函数的函数。
3、反三角函数的求导公式如下: 对于反正弦函数arcsin(x),其导数为1 / √(1 - x)。 对于反余弦函数arccos(x),其导数为-1 / √(1 - x)。 对于反正切函数arctan(x),其导数为1 / (1 + x)。
4、arctanx的导数:y = arctanx,其中 x = tany,因此 dx/dy = secy = tany + 1。由此得到 dy/dx = 1/(dx/dy) = 1/(tany + 1) = 1/(1 + x)。
5、反余弦函数的导数是:dcos^(-1)(x)/dx = -1/√(1 - x^2)。 反正切函数的导数是:dtan^(-1)(x)/dx = 1/(1 + x^2)。 反余切函数的导数是:dcot^(-1)(x)/dx = -1/(1 + x^2)。三角函数是一类基本的初等函数,它们将角度映射到实数比值上。
反三角函数求导
反正弦函数的求导:(arcsinx)=1/√(1-x^2)反余弦函数的求导:(arccosx)=-1/√(1-x^2)反正切函数的求导:(arctanx)=1/(1+x^2)反余切函数的求导:(arccotx)=-1/(1+x^2)三角函数是数学中属于初等函数中的超越函数的函数。
反三角函数求导公式:反余弦函数的导数为(arccosx)=-1/√(1-x^2),反正切函数的导数为(arctanx)=1/(1+x^2)。反三角函数求导过程:对于反正弦函数的求导,设y=arcsinx,则有x=sin(y)。对x=sin(y)进行求导,得到dx/dy=cos(y),因此dy/dx=1/cos(y)。
arctanx的导数:y = arctanx,其中 x = tany,因此 dx/dy = secy = tany + 1。由此得到 dy/dx = 1/(dx/dy) = 1/(tany + 1) = 1/(1 + x)。
反三角函数的求导公式如下: 对于反正弦函数arcsin(x),其导数为1 / √(1 - x)。 对于反余弦函数arccos(x),其导数为-1 / √(1 - x)。 对于反正切函数arctan(x),其导数为1 / (1 + x)。
反三角函数的求导公式如下:y = arctan 的导数为 y = 1/。表示arctan函数对于其内部函数的导数等于x的平方加一的倒数。这个导数基于三角函数的基础性质得出,适用于函数内部的表达式中不含特殊常数或特定复合结构的情况。对于 y = arccos,其导数为 y = -1/。
反正弦函数的求导(arcsinx)=1/√(1-x^2)反余弦函数的求导(arccosx)=-1/√(1-x^2)反正切函数的求导(arctanx)=1/(1+x^2)反余切函数的求导(arccotx)=-1/(1+x^2)为限制反三角函数为单值函数,将反正弦函数的值y限在-π/2≤y≤π/2,将y作为反正弦函数的主值,记为y=arcsin x。
反三角函数的求导公式
1、余割函数y=csc x在[-π/2,0)U(0,π/2]上的反函数,叫做反余割函数。记作arccscx,表示一个余割值为x的角,该角的范围在[-π/2,0)U(0,π/2]区间内。定义域(-∞,-1]U[1,+∞),值域[-π/2,0)U(0,π/2]。
2、反正弦函数的求导:(arcsinx)=1/√(1-x^2)反余弦函数的求导:(arccosx)=-1/√(1-x^2)反正切函数的求导:(arctanx)=1/(1+x^2)反余切函数的求导:(arccotx)=-1/(1+x^2)三角函数是数学中属于初等函数中的超越函数的函数。
3、反三角函数的求导公式如下: 对于反正弦函数arcsin(x),其导数为1 / √(1 - x)。 对于反余弦函数arccos(x),其导数为-1 / √(1 - x)。 对于反正切函数arctan(x),其导数为1 / (1 + x)。
反三角函数求导,怎么求导数?
1、反函数的导数等于直接函数导数的倒数 arccotx=y,即x=coty,左右求导数则有 1=-y*cscy 故y=-1/cscy=-1/(1+coty)=-1/(1+x)。
2、(arccosx)=-1/√(1-x^2)反正切函数的求导 (arctanx)=1/(1+x^2)反余切函数的求导 (arccotx)=-1/(1+x^2)为限制反三角函数为单值函数,将反正弦函数的值y限在-π/2≤y≤π/2,将y作为反正弦函数的主值,记为y=arcsin x。相应地。
3、反正弦函数的导数是:dsin^(-1)(x)/dx = 1/√(1 - x^2)。 反余弦函数的导数是:dcos^(-1)(x)/dx = -1/√(1 - x^2)。 反正切函数的导数是:dtan^(-1)(x)/dx = 1/(1 + x^2)。 反余切函数的导数是:dcot^(-1)(x)/dx = -1/(1 + x^2)。
4、反三角函数的求导公式如下: 对于反正弦函数arcsin(x),其导数为1 / √(1 - x)。 对于反余弦函数arccos(x),其导数为-1 / √(1 - x)。 对于反正切函数arctan(x),其导数为1 / (1 + x)。
5、arctanx的导数:y = arctanx,其中 x = tany,因此 dx/dy = secy = tany + 1。由此得到 dy/dx = 1/(dx/dy) = 1/(tany + 1) = 1/(1 + x)。
反三角函数的求导公式是什么?
1、反三角函数的求导公式:反正弦函数求导:(arcsinx)=1/√(1-x^2);反余弦函数求导:(arccosx)=-1/√(1-x^2);反正切函数求导:(arctanx)=1/(1+x^2);反余切函数求导:(arccotx)=-1/(1+x^2)。
2、反三角函数的求导公式:反正弦的求导:(arcsinx)=1/√(1-x^2)反余弦的求导:(arccosx)=-1/√(1-x^2)反正切的求导:(arctanx)=1/(1+x^2)反余切的求导:(arccotx)=-1/(1+x^2)反三角函数是一种基本初等函数。
3、余割函数y=csc x在[-π/2,0)U(0,π/2]上的反函数,叫做反余割函数。记作arccscx,表示一个余割值为x的角,该角的范围在[-π/2,0)U(0,π/2]区间内。定义域(-∞,-1]U[1,+∞),值域[-π/2,0)U(0,π/2]。
4、反正弦函数的求导:(arcsinx)=1/√(1-x^2)反余弦函数的求导:(arccosx)=-1/√(1-x^2)反正切函数的求导:(arctanx)=1/(1+x^2)反余切函数的求导:(arccotx)=-1/(1+x^2)三角函数是数学中属于初等函数中的超越函数的函数。
5、反三角函数的求导公式如下: 对于反正弦函数arcsin(x),其导数为1 / √(1 - x)。 对于反余弦函数arccos(x),其导数为-1 / √(1 - x)。 对于反正切函数arctan(x),其导数为1 / (1 + x)。
6、反正弦函数的导数是 1 / √(1 - x)。 反余弦函数的导数:反余弦函数的导数是 -1 / √(1 - x)。 反正切函数的导数:反正切函数的导数是 1 / (1 + x)。 反余切函数的导数:反余切函数的导数是 -1 / (1 + x)。