派是无理数吗?怎么证明
证明π是无理数是一个著名的数学成就,它首次由约翰·海因里希·兰伯特在1768年给出。证明π是无理数意味着π不能表示为两个整数的比,即不存在整数p和q(q≠0)使得π = p/q。
上式表示∫f(x)sinxdx在[0,π]区间上的积分为整数,这与(1)式矛盾。所以π不是有理数,又它是实数,故π是无理数。
首先肯定π是无理数。 其次你的想法有误,π的计算机算法是在π是无理数的基础上构建的方法,不是使用割圆法,不存在π=c/d的问题。 最后是证明,涉及到微积分的内容。
在数学中,证明圆周率π是一个无理数是一项重要的挑战。假设π是有理数,我们设π=a/b,其中a和b为自然数。构造函数f(x)=(x^n)[(a-bx)^n]/(n!),当0x1时,f(x)是一个连续且有界的函数。我们观察f(x)在[0,1]区间内的性质。
派是有理数吗?
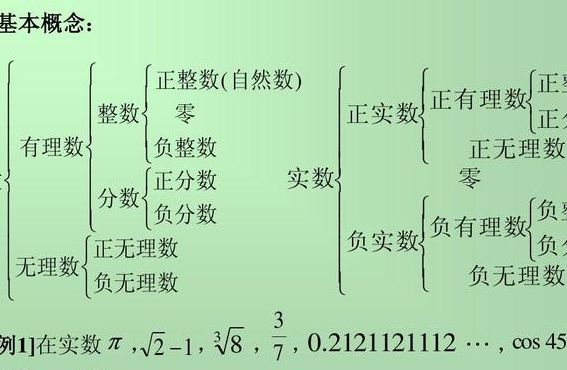
π,即圆周率,是一个无理数。有理数则是整数(包括正整数、0和负整数)与分数的统称。正整数和正分数合称为正有理数,而负整数和负分数合称为负有理数。因此,有理数可以分为正有理数、负有理数和零。有理数可以转化为十进制循环小数,反之亦然,这使得有理数可以被定义为十进制循环小数。
派是不是有理数:π不是有理数。无理数,即非有理数之实数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。π一小数的形式表达时,小数点后的数字无限个,不会循环。
π是无理数。有理数是整数和分数的统称,一切有理数都可以化成分数的形式。无理数,也称为无限不循环小数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。
派(π)是无理数。有理数是可以表示为两个整数相除的形式,即有限小数或无限循环小数。例如,1/3=0.333333,是一个有理数。而派(π)是无理数,因为它无法表示为两个整数相除的形式,无论我们如何尝试。派(π)是一个无理数,只能用无限不循环的小数来表示。
“派”,π也就是圆周率是无理数。有理数为整数(正整数、0、负整数)和分数的统称。正整数和正分数合称为正有理数,负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零。
π不是有理数。因为π=1415926等,是无限不循环小数,不在有理数的范围。有理数包括整数,分数,有限小数,无线循环小数,以及能开得尽方的数。其他的都是无理数。
派是有理数吗
派(π)是无理数。有理数是可以表示为两个整数相除的形式,即有限小数或无限循环小数。例如,1/3=0.333333,是一个有理数。而派(π)是无理数,因为它无法表示为两个整数相除的形式,无论我们如何尝试。派(π)是一个无理数,只能用无限不循环的小数来表示。
π是无理数。有理数是整数和分数的统称,一切有理数都可以化成分数的形式。无理数,也称为无限不循环小数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。
派是不是有理数:π不是有理数。无理数,即非有理数之实数,不能写作两整数之比。若将它写成小数形式,小数点之后的数字有无限多个,并且不会循环。π一小数的形式表达时,小数点后的数字无限个,不会循环。
无理数则是无限不循环小数,无法表示为两个整数之比。无理数在小数表示中没有规律可循,无限且不循环。常见的无理数包括非完全平方数的平方根、π和e(这两个数都是超越数)。无理数的另一个特点是它们具有无限的连分数表达式。无理数的概念最早由毕达哥拉斯学派的弟子希伯索斯发现。
“派”,π也就是圆周率是无理数。有理数为整数(正整数、0、负整数)和分数的统称。正整数和正分数合称为正有理数,负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零。
不是,π是无限不循环无理数。除以3之后还是无理数。有理数为整数(正整数、0、负整数)和分数的统称。正整数和正分数合称为正有理数,负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零。
π是有理数吗?
1、π不是有理数。有理数指的是整数、正整数、负整数、0以及分数,也是整数和分数的集合,比如说整数包含正整数和负整数以及0,所以、-0、、这样的数都是整数也是有理数。但是π等于1415926,是属于无限不循环小数,不在有理数的范围内,所以π不是有理数。
2、上式表示∫f(x)sinxdx在[0,π]区间上的积分为整数,这与(1)式矛盾。所以π不是有理数,又它是实数,故π是无理数。
3、派(π)是无理数。有理数是可以表示为两个整数相除的形式,即有限小数或无限循环小数。例如,1/3=0.333333,是一个有理数。而派(π)是无理数,因为它无法表示为两个整数相除的形式,无论我们如何尝试。派(π)是一个无理数,只能用无限不循环的小数来表示。
4、π不是有理数。因为,根据有理数的定义:有理数是一个整数a和一个正整数b的比,例如3/8,通则为a/b。有理数是整数和分数的集合,整数也可看做是分母为一的分数。有理数的小数部分是有限或为无限循环的数。而π=141592..是无限不循环小数,不在有理数的范围。