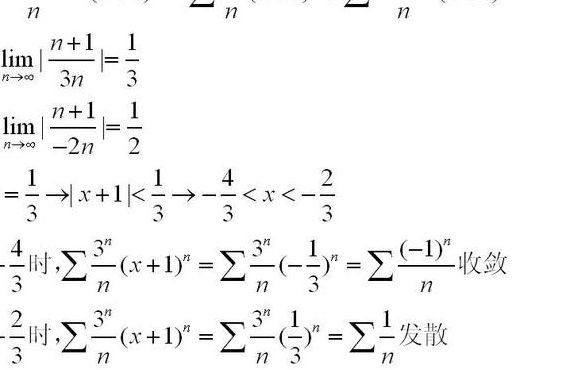收敛半径是怎么求的?
当告诉了x这一点条件收敛时,收敛半径求的过程见上图。结论:如果在x=b处条件收敛,则收敛半径R=|b|。当级数在x一点条件收敛时,用到阿贝尔定理,还用到收敛半径的定义,就可以求出收敛半径了。具体的求收敛半径,此题收敛半径是3。此题求收敛比较的详细步骤及说明见上。
解:∵原式=∑(2/2^n)x^n+∑[(-1/2)^n]x^n,易得∑(2/2^n)x^n、∑[(-1/2)^n]x^n的收敛半径均为R=2,故原级数的收敛半径均为R=2。本题中的等于号应该删去;本题是典型的幂级数(Power series),解答收敛半径的方法有两种:A、比值法;B、根值法。
收敛半径求法是:|z-a|=r。在古典几何中,圆或圆的半径是从其中心到其周边的任何线段,并且在更现代的使用中,它也是其中任何一个的长度。这个名字来自拉丁半径,意思是射线,也是一个战车的轮辐。半径的复数可以是半径(拉丁文复数)或常规英文复数半径。半径的典型缩写和数学变量名称为r。
收敛半径的三种求法如下:根据达朗贝尔审敛法,收敛半径R满足:如果幂级数满足,则:ρ是正实数时,1/ρ。ρ = 0时,+∞。ρ =+∞时,R= 0。根据根值审敛法,则有柯西-阿达马公式:或者。复分析中的收敛半径将一个收敛半径是正数的幂级数的变量取为复数,就可以定义一个全纯函数。
如何求收敛半径?
结论:如果在x=b处条件收敛,则收敛半径R=|b|。当级数在x一点条件收敛时,用到阿贝尔定理,还用到收敛半径的定义,就可以求出收敛半径了。具体的求收敛半径,此题收敛半径是3。此题求收敛比较的详细步骤及说明见上。
确定级数的系数通项表达式;根据系数通项表达式得到第n+1个系数的表达式;利用收敛半径公式,带入系数表达式求收敛半径R;在原级数中带入x=-R判断x=-R处左端点的收敛性;在原级数中带入x=R判断x=R处右端点的收敛性;综合左右端点收敛性和收敛半径得到级数的收敛域。
解:∵原式=∑(2/2^n)x^n+∑[(-1/2)^n]x^n,易得∑(2/2^n)x^n、∑[(-1/2)^n]x^n的收敛半径均为R=2,故原级数的收敛半径均为R=2。本题中的等于号应该删去;本题是典型的幂级数(Power series),解答收敛半径的方法有两种:A、比值法;B、根值法。
收敛半径的三种求法如下:根据达朗贝尔审敛法,收敛半径R满足:如果幂级数满足,则:ρ是正实数时,1/ρ。ρ = 0时,+∞。ρ =+∞时,R= 0。根据根值审敛法,则有柯西-阿达马公式:或者。复分析中的收敛半径将一个收敛半径是正数的幂级数的变量取为复数,就可以定义一个全纯函数。
或者,复分析中的收敛半径将一个收敛半径是正数的幂级数的变量取为复数,就可以定义一个全纯函数。最近点的取法是在整个复平面中,而不仅仅是在实轴上,即使中心和系数都是实数时也是如此。例如:函数没有复根。它在零处的泰勒展开为:运用达朗贝尔审敛法可以得到它的收敛半径为1。
当告诉了x这一点条件收敛时,收敛半径求的过程见上图。结论:如果在x=b处条件收敛,则收敛半径R=|b|。当级数在x一点条件收敛时,用到阿贝尔定理,还用到收敛半径的定义,就可以求出收敛半径了。具体的求收敛半径,此题收敛半径是3。此题求收敛比较的详细步骤及说明见上。
级数收敛半径怎么求?公式是什么?
1、确定级数的系数通项表达式;根据系数通项表达式得到第n+1个系数的表达式;利用收敛半径公式,带入系数表达式求收敛半径R;在原级数中带入x=-R判断x=-R处左端点的收敛性;在原级数中带入x=R判断x=R处右端点的收敛性;综合左右端点收敛性和收敛半径得到级数的收敛域。
2、结论:如果在x=b处条件收敛,则收敛半径R=|b|。当级数在x一点条件收敛时,用到阿贝尔定理,还用到收敛半径的定义,就可以求出收敛半径了。具体的求收敛半径,此题收敛半径是3。此题求收敛比较的详细步骤及说明见上。
3、解:∵原式=∑(2/2^n)x^n+∑[(-1/2)^n]x^n,易得∑(2/2^n)x^n、∑[(-1/2)^n]x^n的收敛半径均为R=2,故原级数的收敛半径均为R=2。本题中的等于号应该删去;本题是典型的幂级数(Power series),解答收敛半径的方法有两种:A、比值法;B、根值法。
4、幂级数收敛半径的两种求法如下:定义法 对任意x\in\mathbf(R)x∈R,定义a_(n)(x)=\frac(x^(n))(n!)an(x)=n!xn。设RR为幂级数的收敛半径,当x=Rx=R时,幂级数成为交错级数。
5、幂级数的收敛半径公式是R=1/ρ。收敛域的求算公式是a(n)/a(n-1)=【n/(n-1)】x,幂级数,是数学分析当中重要概念之一,是指在级数的每一项均为与级数项序号n相对应的以常数倍的(x-a)的n次方(n是从0开始计数的整数,a为常数)。
收敛半径怎么求?
当告诉了x这一点条件收敛时,收敛半径求的过程见上图。结论:如果在x=b处条件收敛,则收敛半径R=|b|。当级数在x一点条件收敛时,用到阿贝尔定理,还用到收敛半径的定义,就可以求出收敛半径了。具体的求收敛半径,此题收敛半径是3。此题求收敛比较的详细步骤及说明见上。
解:∵原式=∑(2/2^n)x^n+∑[(-1/2)^n]x^n,易得∑(2/2^n)x^n、∑[(-1/2)^n]x^n的收敛半径均为R=2,故原级数的收敛半径均为R=2。本题中的等于号应该删去;本题是典型的幂级数(Power series),解答收敛半径的方法有两种:A、比值法;B、根值法。
收敛半径求法是:|z-a|=r。在古典几何中,圆或圆的半径是从其中心到其周边的任何线段,并且在更现代的使用中,它也是其中任何一个的长度。这个名字来自拉丁半径,意思是射线,也是一个战车的轮辐。半径的复数可以是半径(拉丁文复数)或常规英文复数半径。半径的典型缩写和数学变量名称为r。