三角函数余切、正割和余割的关系是什么?
1、首先,我们可以发现余割和正割互为倒数关系。这是因为在直角三角形中,如果一个角的余割是a,那么它的正割就是1/a;反之亦然。这种倒数关系可以通过三角函数的基本性质推导出来。其次,余切和正割也存在着倒数关系。这是因为在直角三角形中,如果一个角的余切是a,那么它的正割就是1/a;反之亦然。
2、总的来说,余割、正割和余切不仅在基本定义上相互关联,而且在函数性质、恒等式和微积分中也形成了错综复杂的数学网。深入理解这些关系,无疑将为我们在解决三角问题、优化计算和理论研究中提供强大的工具。
3、正切(tan)等于对边比邻边;tanA=a/b 余切(cot)等于邻边比对边;cotA=b/a 正割(sec)等于斜边比邻边;secA=h/b 余割(csc)等于斜边比对边。
4、带余切(cot)、正割(sec)和余割(csc)是三角函数的倒数。 带余切(cot):带余切是正切(tan)的倒数。在一个直角三角形中,带余切定义为邻边(直角边)与对边(斜边上除直角边之外的部分)的比值。带余切的公式为:cotθ = 1 / tanθ 正割(sec):正割是余弦(cos)的倒数。
求所有的半角公式和倍角公式
正切的倍角公式:tan(2θ) = (2tanθ) / (1 - tanθ)半角公式:用于计算一个角的一半角的正弦、余弦和正切值。
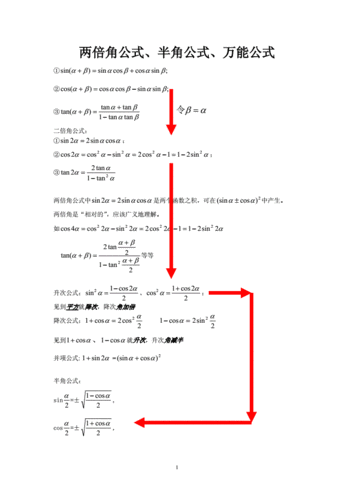
倍角公式和半角公式具体如下:倍角公式 sin2α=2sinαcosα。tan2α=2tanα/(1-tan^2(α))。cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 。半角公式 sin^2(α/2)=(1-cosα)/2。cos^2(α/2)=(1+cosα)/2。
三倍角公式:sin3α=4sinα·sin(π/3+α)sin(π/3-α)。cos3α=4cosα·cos(π/3+α)cos(π/3-α)。tan3a=tana·tan(π/3+a)·tan(π/3-a)。三角函数半角公式:正弦:sin(A/2)=√((1-cosA)/2)。sin(A/2)=-√((1-cosA)/2)。
三角函数半角公式有哪些推导过程
1、半角公式推导过程如下:sin(α+β)=sinacosβ+cosasinβ,当β=α时,得sin2α=2sinαcosα。cos(α+β)=cosacosβ-sinasinβ,当β=α时,得cos2α=2cosα-1=1-2sinα。
2、半角公式如下:三角函数的半角公式:sin(α/2)=±√((1-cosα)/2)。cos(α/2)=±√((1+cosα)/2)。tan(α/2)=±√((1-cosα)/((1+cosα))。三角函数半角公式推导过程:已知公式:sin2α=sin(α+α)=sinαcosα+cosαsinα=2sinαcosα。
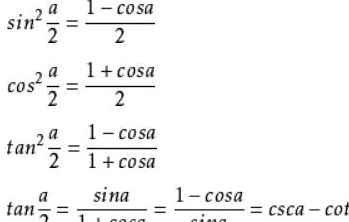
3、半角公式:sin^2(α/2)=(1-cosα)/2 cos^2(α/2)=(1+cosα)/2 tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα 倍角公式和半角公式都是三角函数中非常实用的一类公式。就是把二倍角的三角函数用本角的三角函数表示出来。