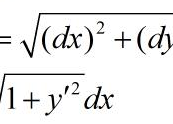高数问题,弧长
1、弧长s=∫√[1+y(x)]dx (x的积分下限a,上限b)下限为a,上限为b,为曲线的端点对应的x的值。弧长:意思为曲线的长度。
2、s=∫ds=∫sqrt((dx)^2+(dy)^2)=∫dx*sqrt(1+(dy/dx)^2)=∫sqrt(1+f^2(x))dx,sqrt()是根号,()^2是()的平方 弧长公式 在半径为 的圆上有一弧(图一),设以 表示它的长,a表示它所对的圆心角,d表示直径,则 这公式右端的 之值,视“角度单位”的选择而变更。
3、下限a,上限b,为曲线的端点对应的x的值。弧长:指曲线的长度。
积分弧长公式
1、弧长s=∫根号下[1+y(x)]dx。弧长公式中下限为a,上限为b,ab为曲线的端点对应的x的值,弧长意思为曲线的长度。定积分是积分的一种,是函数f(x)在区间[a,b]上积分和的极限。曲线积分分为:对弧长的曲线积分和对坐标轴的曲线积分。两种曲线积分的区别主要在于积分元素的差别。
2、弧长s=∫√[1+y(x)]dx (x的积分下限a,上限b)下限为a,上限为b,为曲线的端点对应的x的值。弧长:意思为曲线的长度。
3、积分弧长公式是描述曲线弧长的公式,L表示曲线的弧长,[a,b]是曲线的定义域,而dy/dx则是曲线在每一点处的斜率。积分弧长公式是对曲线的方程进行积分来求出该曲线的弧长。原理是将曲线分解成无数个微小的线段,然后对每个微小的线段求出其长度,再将所有的长度加起来,就得到了整个曲线的弧长。
4、曲线弧长积分公式:ds=√(dx+dy),在数学中,曲线积分是积分的一种。积分函数的取值沿的不是区间,而是特定的曲线,称为积分路径。曲线积分有很多种类,当积分路径为闭合曲线时,称为环路积分或围道积分。曲线积分可分为:第一类曲线积分和第二类曲线积分。
5、定积分的应用弧长公式是L=∫[a,b]√(1+(dy/dx))dx。设有一条曲线y=f(x),我们希望求解曲线上两点之间的弧长。我们可以将曲线分割成许多小段,每一小段可以看作是一条直线段,然后计算每一小段的长度,最后将所有小段的长度相加即可得到整个曲线的弧长。
弧长积分公式是什么?
1、曲线弧长积分公式:ds=√(dx+dy),在数学中,曲线积分是积分的一种。积分函数的取值沿的不是区间,而是特定的曲线,称为积分路径。曲线积分有很多种类,当积分路径为闭合曲线时,称为环路积分或围道积分。曲线积分可分为:第一类曲线积分和第二类曲线积分。
2、弧长公式积分是∫f(x,y)ds。积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种。直观地说,对于一个给定的正实值函数,在一个实数区间上的定积分可以理解为在坐标平面上,由曲线、直线以及轴围成的曲边梯形的面积值(一种确定的实数值)。
3、微积分弧长计算公式:L=n×π×r/180,L=α×r。其中n是圆心角度数(角度制),r是指半径,L是圆心角弧长,α是圆心角度数(弧度制)。
弧长计算公式微积分
微积分弧长计算公式:L=n×π×r/180,L=α×r。其中n是圆心角度数(角度制),r是指半径,L是圆心角弧长,α是圆心角度数(弧度制)。
高数弧长ds的三种公式:s=∫ds=∫sqrt((dx)^2+(dy)^2)=∫dx*sqrt(1+(dy/dx)^2)=∫sqrt(1+f^2(x))dx。sqrt()是根号,()^2是()的平方。
这两个公式都是用来计算弧长的,选择使用哪个公式取决于你使用的角度单位。如果你使用角度制(度数),则使用第一个公式;如果你使用弧度制,则使用第二个公式。弧长公式也是微积分学中用来计算曲线长的基本公式之一。弧长公式的应用非常广泛,例如在物理学、工程学、经济学等领域中都有应用。
y`=[(2/3)x^(3/2)]`=√x 代入弧长公式,得 s=∫√(1+y`)dx =∫√(1+x)dx =(2/3)(1+x)^(3/2)。
你好!弧长公式 s = ∫(a,b) √ { 1+ [ f(x) ] } dx 推导过程就是无限分割,每一小段看作线段,再求和 式子比较复杂,这里打不出来,你自己试着推导吧。
曲线弧长计算公式:L=n×π×r/180。曲线,是微分几何学研究的主要对象之一。直观上,曲线可看成空间质点运动的轨迹。微分几何就是利用微积分来研究几何的学科。为了能够应用微积分的知识,我们不能考虑一切曲线,甚至不能考虑连续曲线,因为连续不一定可微。曲线的弧长也称曲线的长度,是曲线的特征之一。
求解释!急!!!定积分的应用,弧长公式!
定积分的应用弧长公式是L=∫[a,b]√(1+(dy/dx))dx。设有一条曲线y=f(x),我们希望求解曲线上两点之间的弧长。我们可以将曲线分割成许多小段,每一小段可以看作是一条直线段,然后计算每一小段的长度,最后将所有小段的长度相加即可得到整个曲线的弧长。
定积分求平面曲线弧长公式:ds=√(1+y^2)dx。定积分作为积分的一种。是函数f(x)在区间[a,b]上积分和的极限。这里应注意定积分与不定积分之间的关系:若定积分存在,则它是一个具体的数值,而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式)。
定积分求平面曲线弧长公式: ds=√(1+y^2)dx;定积分作为积分的一种,是函数f(x)在区间[a,b]上积分和的极限。这里应注意定积分与不定积分之间的关系:若定积分存在,则它是一个具体的数值,而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式)。
如下:弧长s=∫根号下[1+y(x)]dx。弧长公式中下限为a,上限为b,ab为曲线的端点对应的x的值,弧长意思为曲线的长度。定积分是积分的一种,是函数f(x)在区间[a,b]上积分和的极限。曲线积分分为:对弧长的曲线积分和对坐标轴的曲线积分。两种曲线积分的区别主要在于积分元素的差别。