向心加速度公式推导是什么?
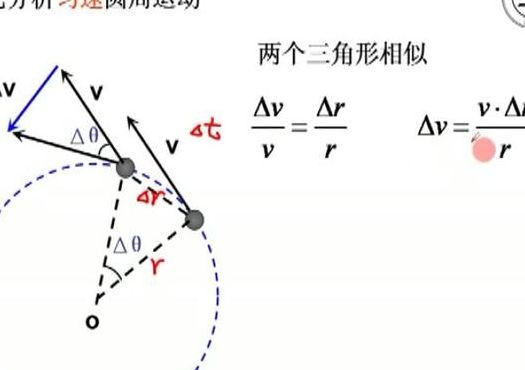
1、向心加速度公式推导是设做匀速圆周运动的物体的线速度的大小为v ,轨迹半径为r。经过时间△t,物体从A点运动到B点。尝试用v 、r 写出向心加速度的表达式。
2、向心加速度的公式:an=Fn/m=4πR/T=4πfR=v/R=ωR=vω。
3、圆周运动的加速度公式可以通过向心加速度的概念推导得出。向心加速度是指物体在做圆周运动时由于改变方向而产生的加速度。
4、由余弦定理可得 可见当θ→0时,α=90°,即△v的方向和vb垂直,由于vb方向为圆周切线方向,故△v的方向指向圆心.因△v的方向即为加速度的方向,可见匀速圆周运动中加速度的方向指向圆心, 。
5、加速度的方向是时刻改变的,所以圆周运动一定是变加速运动。可理解为做圆周运动物体加速度在指向圆心(曲率中心)方向上的分量。向心加速度是矢量,并且它的方向无时无刻不在改变且指向圆心(曲率中心)。
如何推导出向心加速的公式?
角加速度计算公式如下:角速度的计算公式为: ω = Δθ / Δt。加速度角速度时间的关系:质点绕某轴转动时,角速度也可能随时间变化,把单位时间内角速度的变化量叫做角加速度。
由余弦定理可得 可见当θ→0时,α=90°,即△v的方向和vb垂直,由于vb方向为圆周切线方向,故△v的方向指向圆心.因△v的方向即为加速度的方向,可见匀速圆周运动中加速度的方向指向圆心, 。
所以a∝v^2/r。质点作曲线运动时,指向圆心(曲率中心)的加速度,与曲线切线方向垂直,也叫做法向加速度。向心加速度是反映圆周运动速度方向变化快慢的物理量。向心加速度只改变速度的方向,不改变速度的大小。
a = F / m1 结合以上两个公式,可以得出天体的向心加速度公式:a = G x m2 / r其中m2是另一个天体的质量,r是两个天体之间的距离。
向心加速度公式
向心加速度的公式是a(n)=W·V,其中a(n)表示向心加速度,W表示物体圆周运动的角速度,V表示物体圆周运动的线速度(切向速度)。向心加速度也叫法向加速度,表示的是质点作曲线运动时,指向圆心(曲率中心)的加速度。
向心加速度的公式:an=Fn/m=4πR/T=4πfR=v/R=ωR=vω。
公式:a向=rω^2=v^2/r=4π^2r/T^2 所有做曲线运动的物体都有向心加速度,向心加速度反映线速度方向变化的快慢。向心加速度又叫法向加速度,意思是指向曲线的法线方向的加速度。
向心加速度公式:a向=v^2/r=ω^2r=(4π^2r)/(T^2)=4π^2f^2r=vω=F向/m。由牛顿第二定律,力的作用会使物体产生一个加速度。合外力提供向心力,向心力产生的加速度就是向心加速度。
向心加速度: a(n)=V/r。a(n)表示向心加速度,v表示物体圆周运动的线速度(切向速度),r表示物体圆周运动的半径。质点作曲线运动时,指向圆心(曲率中心)的加速度,与曲线切线方向垂直,也叫做法向加速度。
向心加速度是物体在做圆周运动时所受到的加速度,它是使物体保持在圆周运动轨迹上的力。
向心加速度公式推导
向心加速度公式推导如下:向心加速度公式:a向=v^2/r=ω^2r=4π^2r/T^2=4π^2f^2r=vω=F向/m。由牛顿第二定律,力的作用会使物体产生一个加速度。合外力提供向心力,向心力产生的加速度就是向心加速度。
a = - ((2πr) / T)^2 / r 对公式进行简化和化简,得到最终的向心加速度公式:a = - (4π^2r) / T^2 这就是圆周运动的加速度公式。
矢量合成法如图1所示,物体自半径为r的圆周a匀速率运动至b,所经时间为△t,若物体在a、b点的速率为va=vb=v,则其速度的增量△v=vb-va=vb+(-va),由平行四边形法则作出其矢量图如图1。