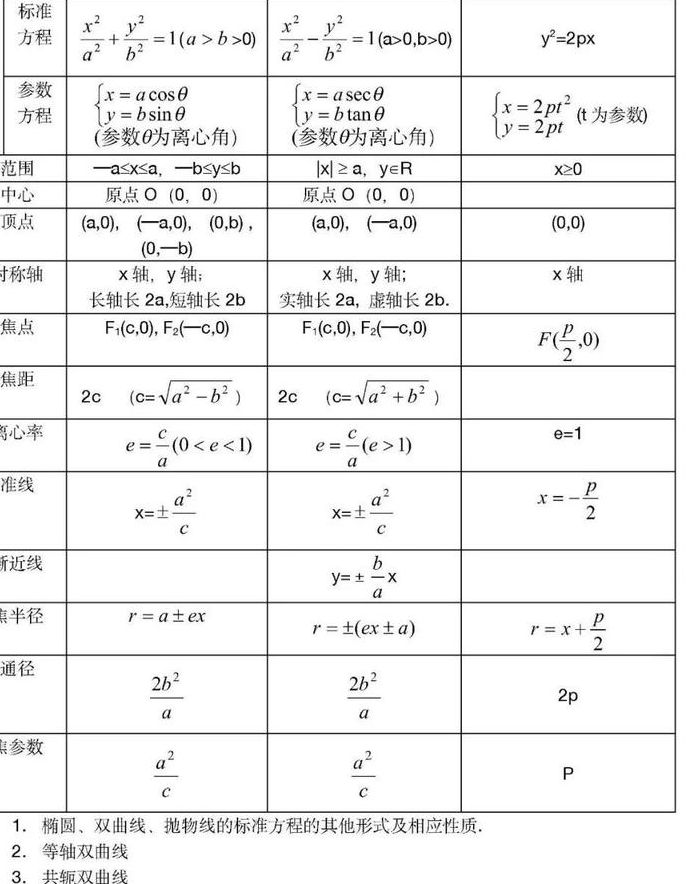
圆锥曲线的知识点及解题方法?
1、牢记核心知识,例如椭圆、双曲线离心率公式和范围,焦点分别在x轴、y轴上的双曲线的渐近线方程等。计算能力与速度。计算能力强的同学学圆锥曲线相对轻松一些,计算能力是可以通过多做题来提升的。
2、解题技巧和方法:掌握一些解题技巧和方法,如代数化、变量替换、三角换元等,提高解题效率和准确性。综合运用:能够将圆锥曲线的知识与其他数学知识相结合,解决复杂的数学问题。这需要具备较强的数学素养和逻辑思维能力。
3、注意审题和分析:在解题过程中,我们需要仔细审题,理解题目的要求,分析问题的关键点。对于一些复杂的问题,我们可以尝试将其分解为几个简单的问题,逐一解决。
高考圆锥曲线部分有哪些知识点?
1、当平面与二次锥面的母线平行,且不过圆锥顶点,结果为抛物线。当平面与二次锥面的母线平行,且过圆锥顶点,结果退化为一条直线。当平面只与二次锥面一侧相交,且不过圆锥顶点,结果为椭圆。
2、圆锥曲线知识点如下:平面内,到给定一点及一直线的距离之比为常数e(e1,即为双曲线的离心率;定点不在定直线上)的点的轨迹称为双曲线。定点叫双曲线的焦点,定直线叫双曲线的准线。
3、高中圆锥曲线是数学中的一个重要概念,它包括椭圆、双曲线和抛物线。这些曲线在几何性质上有很多相似之处,因此容易混淆。
4、圆锥曲线知识点有如下:圆锥曲线中,过焦点并垂直于轴的弦成为通径。到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。当0e1时为椭圆:当e=1时为抛物线;当e1时为双曲线。
圆锥曲线的高中知识点有哪些?
焦点与准线:椭圆有两个焦点,每个焦点对应一条准线;双曲线有两个焦点,每个焦点对应两条准线;抛物线只有一个焦点,没有准线。离心率:椭圆的离心率小于1;双曲线的离心率大于1;抛物线的离心率为1。
圆锥曲线知识点如下:平面内,到给定一点及一直线的距离之比为常数e(e1,即为双曲线的离心率;定点不在定直线上)的点的轨迹称为双曲线。定点叫双曲线的焦点,定直线叫双曲线的准线。
在学习圆锥曲线时,需要掌握以下几个方面的知识:二次函数的图像及性质,如对称轴、顶点、焦点、准线等。椭圆、双曲线和抛物线的标准方程、性质、图像及相关概念,如离心率、直线的位置、渐近线等。
圆锥曲线知识点有如下:圆锥曲线中,过焦点并垂直于轴的弦成为通径。到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。当0e1时为椭圆:当e=1时为抛物线;当e1时为双曲线。
高中数学圆锥曲线基础知识 定义 圆锥曲线包括圆,椭圆,双曲线,抛物线。其统一定义:到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。当e1时为双曲线,当e=1时为抛物线,当e1时为椭圆。
圆锥曲线知识点有哪些?
1、圆锥曲线知识点如下:平面内,到给定一点及一直线的距离之比为常数e(e1,即为双曲线的离心率;定点不在定直线上)的点的轨迹称为双曲线。定点叫双曲线的焦点,定直线叫双曲线的准线。
2、切线和法线:圆锥曲线上的点到其主轴线的切线和法线可以通过导数和斜率计算。焦半径:焦半径是从焦点到曲线上任意一点的线段。对于椭圆和双曲线,焦半径的长度可以通过勾股定理计算。曲率:曲率是描述曲线弯曲程度的量。
3、圆锥曲线知识点如下:弦中点问题,端点坐标设而不求。当平面只与二次锥面一侧相交,且不过圆锥顶点,并与圆锥的对称轴垂直,结果为圆。平面内一个动点到一个定点与一条定直线的距离之比是一个大于1的常数e。
4、圆锥曲线知识点有如下:圆锥曲线中,过焦点并垂直于轴的弦成为通径。到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。当0e1时为椭圆:当e=1时为抛物线;当e1时为双曲线。
5、圆锥曲线的统一定义:到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。当0e1时为椭圆:当e=1时为抛物线;当e1时为双曲线。圆锥曲线的方程。
6、定点叫做该圆锥曲线的焦点,定直线叫做(该焦点相应的)准线,e叫做离心率。
圆锥曲线知识点总结
圆锥曲线知识点如下:平面内,到给定一点及一直线的距离之比为常数e(e1,即为双曲线的离心率;定点不在定直线上)的点的轨迹称为双曲线。定点叫双曲线的焦点,定直线叫双曲线的准线。
高考数学常用的圆锥曲线知识点总结 椭圆: (1)椭圆的定义:平面内与两个定点f1,f2的距离的和等于常数(大于|其中:两个定点叫做椭圆的焦点,焦点间的距离叫做焦距。
圆锥曲线知识点如下:弦中点问题,端点坐标设而不求。当平面只与二次锥面一侧相交,且不过圆锥顶点,并与圆锥的对称轴垂直,结果为圆。平面内一个动点到一个定点与一条定直线的距离之比是一个大于1的常数e。
定点叫做该圆锥曲线的焦点,定直线叫做(该焦点相应的)准线,e叫做离心率。