单纯形法计算步骤详解
1、在开始单纯形法计算之前,首先需要基于约束条件方程组的系数矩阵,通过寻找或构造单位矩阵的方法,来确定基变量,从而求出初始基本可行解。这个步骤中,我们需要利用初始基本可行解及线性规划模型提供的信息,编制初始单纯形表。这个初始单纯形表将成为我们后续计算的基础。
2、关于这个问题,单纯形法的计算步骤如下: 将标准型线性规划问题表示成矩阵形式。 根据标准型线性规划问题的矩阵形式构造初始可行解。 计算初始可行解的目标函数值,如果是最小化问题,则将目标函数系数取相反数。 如果初始可行解是最优解,则直接输出结果。
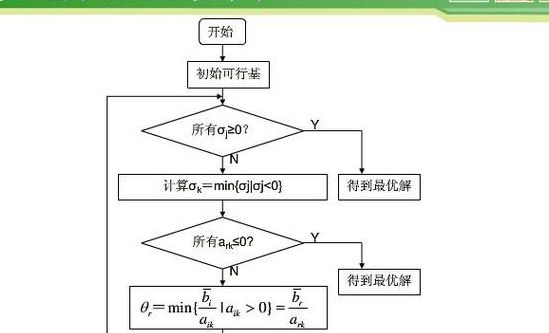
3、单纯形法的一般解题步骤包括:将线性规划问题的约束方程组表达成典范型方程组,找出基本可行解作为初始基本可行解。若存在可行解,则从初始基本可行解作为起点,通过引入非基变量取代某一基变量,寻找目标函数值更优的另一基本可行解。迭代进行,直到检验数满足最优性条件或目标函数值无界。
单纯形法求解过程
1、在开始单纯形法计算之前,首先需要基于约束条件方程组的系数矩阵,通过寻找或构造单位矩阵的方法,来确定基变量,从而求出初始基本可行解。这个步骤中,我们需要利用初始基本可行解及线性规划模型提供的信息,编制初始单纯形表。这个初始单纯形表将成为我们后续计算的基础。
2、方法步骤:把线性规划问题的约束方程组表达成典范型方程组,找出基本可行解作为初始基本可行解。若基本可行解不存在,即约束条件有矛盾,则问题无解。
3、单纯形法的一般解题步骤包括:将线性规划问题的约束方程组表达成典范型方程组,找出基本可行解作为初始基本可行解。若存在可行解,则从初始基本可行解作为起点,通过引入非基变量取代某一基变量,寻找目标函数值更优的另一基本可行解。迭代进行,直到检验数满足最优性条件或目标函数值无界。
4、求解过程如下图 此时所有Cj-Zj≤0,已得到最优解。
5、接下来,我们使用单纯形法进行求解。单纯形表的构造与计算过程较为复杂,但通过这一方法,我们可以逐步优化目标函数,直到找到最优解。经过计算,我们得到最小化目标函数的最优值minw = 140000/3。此时的最优解为x = (200, 400/3)’。以上是单纯形法求解该线性规划问题的基本步骤。
6、x2,x3 = 0 接下来使用单纯形法进行求解。
单纯形法检验数怎么算
单纯形法检验数计算方法是:用基变量在目标函数中的系数,乘以要算得那个变量对应的系数列的各个值,并求和,再减去要算得那个变量在目标函数中对应的系数,就是检验数。
在目标函数中用非基变量代替基变量,所得系数即是检验数。在目标规划中,p1p2p3不是具体算出来的值,而是按照原先的方法在草纸上写出计算校验数的式子,系数有p1p2p3就带着,整理会得到一个关于p1p2p3的式子,那一列填的就是这个式子中p1p2p3的系数,就这样一列一列就可以填好。
在目标函数中用非基变量代替基变量,所得系数即是检验数。根据目标函数中非基变量的系数,乘以你要算得那个变量对应的系数列的各个值,并求和。再减去要算得那个变量在目标函数中对应的系数,就是检验数。
在单纯形法中,检验数的计算是至关重要的步骤。具体计算方法是:首先,将基变量在目标函数中的系数与要计算的变量对应的系数列的各个值相乘,并对这些乘积求和。然后,从上述和中减去要计算的变量在目标函数中对应的系数,即可得到该变量的检验数。
单纯形法的计算步骤
单纯形法的一般解题步骤包括:将线性规划问题的约束方程组表达成典范型方程组,找出基本可行解作为初始基本可行解。若存在可行解,则从初始基本可行解作为起点,通过引入非基变量取代某一基变量,寻找目标函数值更优的另一基本可行解。迭代进行,直到检验数满足最优性条件或目标函数值无界。
关于这个问题,单纯形法的计算步骤如下: 将标准型线性规划问题表示成矩阵形式。 根据标准型线性规划问题的矩阵形式构造初始可行解。 计算初始可行解的目标函数值,如果是最小化问题,则将目标函数系数取相反数。 如果初始可行解是最优解,则直接输出结果。
在单纯形法中,检验数的计算是至关重要的步骤。具体计算方法是:首先,将基变量在目标函数中的系数与要计算的变量对应的系数列的各个值相乘,并对这些乘积求和。然后,从上述和中减去要计算的变量在目标函数中对应的系数,即可得到该变量的检验数。
在开始单纯形法计算之前,首先需要基于约束条件方程组的系数矩阵,通过寻找或构造单位矩阵的方法,来确定基变量,从而求出初始基本可行解。这个步骤中,我们需要利用初始基本可行解及线性规划模型提供的信息,编制初始单纯形表。这个初始单纯形表将成为我们后续计算的基础。
单纯形法检验数计算方法是:用基变量在目标函数中的系数,乘以要算得那个变量对应的系数列的各个值,并求和,再减去要算得那个变量在目标函数中对应的系数,就是检验数。
其基本步骤和单纯形法大致相同,主要区别是在逐次迭代中不再以高斯消去法为基础,而是由旧基阵的逆去直接计算新基阵的逆,再由此确定检验数。这样做可以减少迭代中的累积误差,提高计算精度,同时也减少了在计算机上的存储量。
运筹学专业课考点丨单纯形的计算步骤:单纯形表
基础构建 首先,我们需要确定初始的基变量,这些是决定问题基本结构的变量。同时,计算每个非基变量的价值系数,这将帮助我们理解它们在当前状态下的重要性。基础变量与约束常数的组合形成单纯形表的核心部分。
表格第一行,分别为目标函数变量的所有系数 表格第二行,left部分,有三项Cb,Xb,b 。right部分,是所有变量(包括基本变量,剩余变量,松弛变量,人工变量)。表格最后一行,为目标函数-Z。Z的计算:变量的目标函数系数-Cb*约束函数变量的系数,然后求和。
学运筹学的入门步骤是掌握线性代数的基础。单纯形表法是一种求解线性规划问题的有效方法,这里简要介绍一下它的操作流程: 首先,将目标函数中的系数取相反数,即min后的部分,这一行也被称为检验数行。 接着,将检验数行下面的矩阵调整为含有单位矩阵的形式,即所有元素为1和0。
这个步骤主要是为了将问题转换为数学形式,便于后续计算。单纯形表通常包括目标函数、约束条件和基变量等关键信息。建立表格之后,需要逐步进行替换操作,通过一系列迭代过程来优化目标函数值。具体而言,这包括选择进基变量和出基变量,从而调整基变量的值,直到达到最优解。