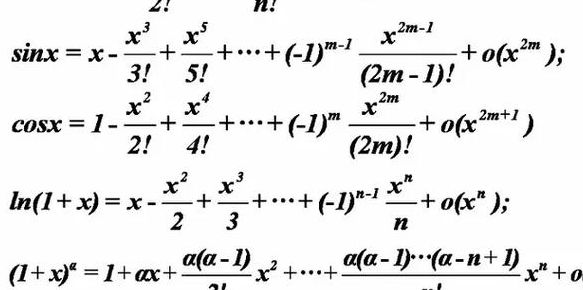泰勒公式是什么?
1、泰勒公式就是将函数用多项式表达的一种通用方法,又称为泰勒展开。看起来高端大气,如果a=0的话,就是麦克劳伦公式。泰勒公式一句话描述:就是用多项式函数去逼近光滑函数。泰勒公式是什么?泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。
2、泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。
3、泰勒公式是函数展开的一种方式,即把一个函数在某一点的邻域内展开成一个多项式形式。下面就为您详细介绍一下常见的泰勒公式。一阶泰勒公式\nf(x)=f(a)+f′(a)(xa)其中f(a)为f(x)在x=a处的函数值,f′(a)为f(x)在x=a处的导数。
4、泰勒公式(Taylor series)是一种数学工具,它能将一个复杂的函数表示为无限级数的形式,便于进行计算和分析。它的基本思想是将函数分解成无限个项的和,每个项由函数在某一点的导数来表示。
5、对数ln(1+x)的泰勒公式是:ln(1+x)=x-x^2\2+x^3\3-x^4\4+1)^(n-1)x^n\n+O(x^(n+1)),泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。
泰勒展开的六种形式?
常用泰勒展开公式如下:sinx=x-1/6x^3+o(x^3),这是泰勒公式的正弦展开公式,在求极限的时候可以把sinx用泰勒公式展开代替。arcsinx=x+1/6x^3+o(x^3),这是泰勒公式的反正弦展开公式,在求极限的时候可以把arcsinx用泰勒公式展开代替。
常用六个泰勒展开公式如下:(e^x=1+x+frac(x^2)(2!)+frac(x^3)(3!)+frac(x^4)(4!)+dots)。(sin(x)=x-frac(x^3)(3!)+frac(x^5)(5!)-frac(x^7)(7!)+dots)。
常用的泰勒展开公式如下:Rn(x) = o((x-a)^n)。Rn(x) = f(n+1)(a+θ(x-a))(1-θ)^(n+1-p)(x-a)^(n+1)/(n!p)。
正弦函数的泰勒展开式:sinx = x - x^3/3! + x^5/5! - ...。这是对正弦函数sinx的泰勒展开形式。这一展开式常用于三角函数的近似计算。 余弦函数的泰勒展开式:cosx = 1 - x^2/2! + x^4/4! - ...。
泰勒公式是数学中一种强大的工具,它允许我们通过函数在某点的导数值来近似表达其在该点附近的复杂行为。以下是八个常见的泰勒公式展开形式: 对于正弦函数sinx,其泰勒展开为x - 1/6x^3 + o(x^3),在求极限时,sinx可以用这个公式进行替换。
8个常用泰勒公式展开图片
1、个常用泰勒公式,如下图所示:在数学中,泰勒级数用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。相关信息:泰勒公式得名于英国数学家布鲁克·泰勒。他在1712年的一封信里首次叙述了这个公式,尽管1671年詹姆斯·格雷高里已经发现了它的特例。
2、个常用泰勒公式如下图:泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。在数学中,泰勒级数用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。
3、个常用泰勒公式展开图如下:e^x=1+x+x^2/2!+x^3/3!+……+x^n/n!+……。ln(1+x)=x-x^2/2+x^3/3-……+(-1)^(k-1)*(x^k)/k(|x|1)。sinx=x-x^3/3!+x^5/5!-……+(-1)^(k-1)*(x^(2k-1))/(2k-1)!+……。(-∞x∞)。
4、个常用泰勒公式,如下图所示:在数学中,泰勒级数用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。
5、常用泰勒展开公式如下:sinx=x-1/6x^3+o(x^3),这是泰勒公式的正弦展开公式,在求极限的时候可以把sinx用泰勒公式展开代替。arcsinx=x+1/6x^3+o(x^3),这是泰勒公式的反正弦展开公式,在求极限的时候可以把arcsinx用泰勒公式展开代替。