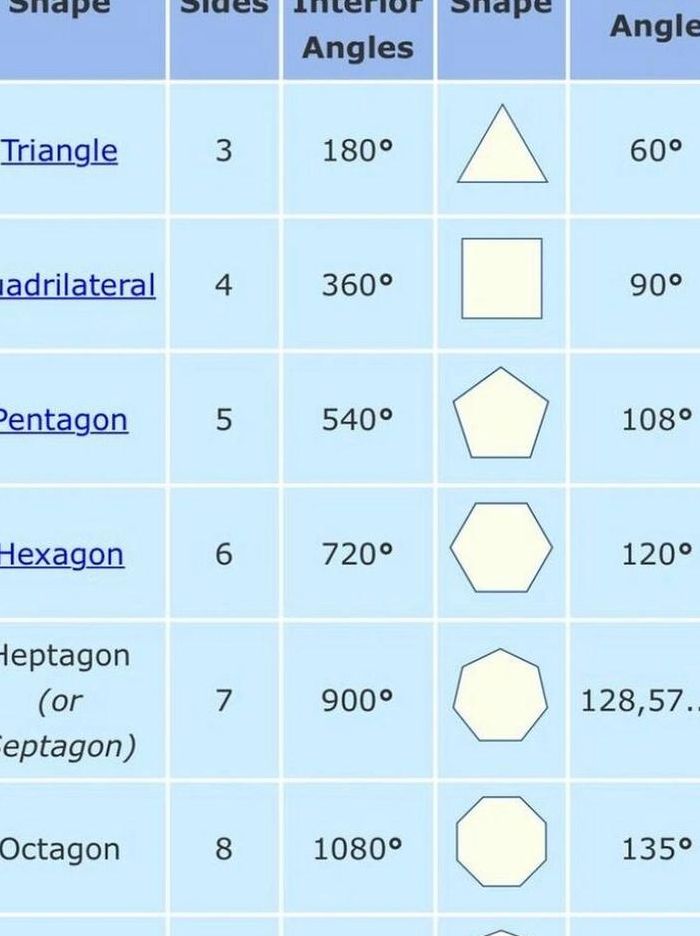
六边形的每个内角是多少度?
1、因此,正六边形的每个内角是120度。正六边形面积的计算公式: 正六边形可以被分割成六个全等的正三角形,每个正三角形以正六边形的中心为顶点,两条相邻边为底边。 在正三角形中,高可以通过以下方式计算:高 = 边长 × √3 / 2。
2、正六边形内角和为720,一个内角为120度。六边形,多边形的一种,指所有有六条边和六个角的多边形。根据正多边形内角和公式S=180°·(n-2),所有的正六边形的内角和都是720°,外角和为360°。正六边形就是在平面几何学中,具有六条相等的边和六个相等内角的多边形。各内角相等,六边相等。
3、正六边形的内角和为720度,每个内角为120度。正六边形在几何学中指的是六条边等长且六个内角也相等的多边形。由于多边形外角和恒等于360度,所以每个内角可通过计算得到,即180度减去外角360度除以6,得出每个内角为120度。雪晶的六角形状可分为片状和柱状两大类。
一个正6边形的每个内角是多少度
正六边形每个内角等于180度乘6分之括号6减2,等于180度乘3分之2,等于120度。所以正六边形每个内角是128度。
正六边形内角和为720,一个内角为120度。六边形,多边形的一种,指所有有六条边和六个角的多边形。根据正多边形内角和公式S=180°·(n-2),所有的正六边形的内角和都是720°,外角和为360°。正六边形就是在平面几何学中,具有六条相等的边和六个相等内角的多边形。各内角相等,六边相等。
正六边形的内角和是720度,每一个内角为120度。正六边形是一种具有六个等边和六个等角的几何图形。在多边形中,内角和是指所有内角的总和。对于正六边形而言,由于所有的边和角都是相等的,我们可以使用特定的数学公式来计算其内角和。具体如下:一个正六边形有六个内角。
正六边形的外角和等于360度,因此一个正六边形的内角是120度。 正六边形是平面几何中一种具有六条相等边和六个相等内角的多边形,其中每个内角都相等。 在生活中,正六边形的形状常见于雪晶和蜂巢。 蜂巢由无数个大小相同的房孔组成,每个房孔都是正六角形,并且每个房孔都相邻于其他房孔。
正六边形的一个内角为120度。正六边形就是在平面几何学中,具有六条相等的边和六个相等内角的多边形。各内角相等,六边相等。由多边形外角和等于360度,推出一个内角为180-(360/6)=120度,所以内角为120度。
正六边形每个内角的度数是多少?还有多边形的内角和及每个内角的度数的公...
1、正六边形的内角度数为120度。可以这样速算,从两个相对的顶点引条线,就把正六边形分成两个梯形,每个四边形的内角和为360,所以正六边形内角和就为720,再除以六。多边形的内角和公式为:(n-2)*180,每个内角度数就是(n-2)*180/n。其实也就是在三角形的基础上每多一条边,内角就增加180。
2、一个正六边形的每个内角是120度。多边形求角的度数的公式如下:多边形的内角和等于180度乘括号n减2。每个内角的度数等于180度乘n分之括号n减2。所以正六边形内角和等于180度乘括号6减2,等于180度乘4,等于720度。所以正六边形内角和等于720度。
3、由于正六边形有六个内角,每个内角的度数就是:720°÷6=120°。所以,正六边形每个内角的度数是120°。在数学中,正多边形内角的计算是一个基础而重要的概念。它涉及到几何学、代数学和基础算术等多个领域的知识。通过掌握如何计算正多边形的内角,我们可以更好地理解和解决与几何图形相关的问题。
4、正六边形的每个内角的度数是120°。根据多边形的内角和定理可得:正六边形的每个内角的度数=(6-2)×180°÷6=120°。正六边形就是在平面几何学中,具有六条相等的边和六个相等内角的多边形。各内角相等,六边相等。
5、答案就是正六边形的内角和是720°,每个内角为120°。六边形可分成4个三角形,每个三角形内角和是180°,所以六边形的内角和为180°×4=720°;正六边形的6个内角相等,所以每个内角为720°÷6=120°。