反函数的公式有哪些?(要全)
所以,那么变量x是变量y的函数.这个函数用来表示,称为函数的反函数.(1) 由原函数y=f(x)求出它的值域; (2) 由原函数y=f(x)反解出x=f-1(y);(3) 交换x,y改写成y=f-1(x);(4) 用f(x)的值域确定f-1(x)的定义域。
先判读这个函数是否为单调函数,若非单调函数,则其反函数不存在。设y=f(x)的定义域为D,值域为f(D)。
反函数公式是:如果函数f(x)在区间[a,b]上是单调的,并且存在反函数f^(-1)(x),那么反函数的公式为f^(-1)(y) = x,其中y = f(x),x [a,b]。详细来说,反函数是一种特殊的函数,它是原函数的逆运算。
动作识别算法
动作识别任务定义:视频动作识别的输入是视频片段,通过将其采样为若干帧进行动作类别识别,本质上是视频分类任务。 下游应用:包括时序动作定位、时空动作定位、检测、视频文本检索与对齐、视频问答、零样本动作识别、开放集动作识别等。
在特征提取后,我们选择支持向量机(SVM)作为初始算法,结果准确率达到100%,随后我们采用了随机森林算法作为核心算法,以适应实际测试中的情况。通过随机森林算法,我们可以实现对动作的高准确率识别。在项目实现中,我们绘制了一块拓展64kRAM的PCB电路板,并打印出实物图。
技术原理分为两大部分:人体骨架提取与动作识别。首先,通过图像处理算法从视频或深度数据中提取人体骨架信息,包括关键点和连接关键点的边。其次,使用机器学习或深度学习算法,尤其是卷积神经网络(CNN)、循环神经网络(RNN)和长短时记忆网络(LSTM)对提取信息进行分类识别。
光流法 光流法是一种基于运动信息的方法,它通过计算图像中像素或特征点的运动速度来识别行为。这种方法对摄像头的视角变化有一定的适应性,因此被广泛应用于实际场景中的行为识别。
本文主要整理了近五年来在第一类方法中的算法,包括two-stream(双流)方法、C3D方法及CNN-LSTM方法,并从算法介绍、架构、参数配置、训练集预处理、算法优势及原因、运行结果六个方面进行详细阐述,对每个分支算法的集合总结心得。本文不区分行为识别(Activity Recognition)与动作识别(Action Recognition)。
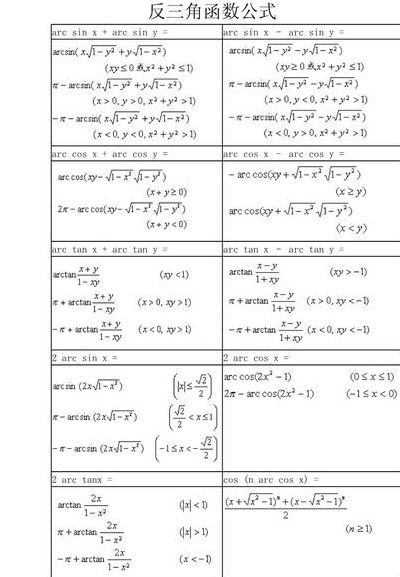
反三角函数公式有哪些?
反三角函数包含12个基本公式,其中一些较为基础的公式包括: 对于任意x,arcsin(-x)等于-arcsinx。 对于任意x,arctan(-x)等于-arctanx。 对于任意x,arccot(-x)等于π-arccotx。
三角函数的反函数是个多值函数,因为它并不满足一个自变量对应一个函数值的要求,其图像与其原函数关于函数 y=x 对称。欧拉提出反三角函数的概念,并且首先使用了“arc+函数名”的形式表示反三角函数。关于反三角函数的计算公式比较多。
反三角函数是一类与基本三角函数互为逆运算的函数,它们之间的关系可以通过以下公式来表示: cos(反余弦x) = √(1 - x^2),这意味着当知道一个角的余弦值时,可以反向计算出对应的角度。 反正弦(-x) = -反正弦x,这表明正弦值的符号变化会导致角度取相反的值。
如何求反函数的导数?
求反函数导数的方法:直接法:这种方法是最直观也是最常用的。首先,我们需要找到原函数的反函数,然后对其进行求导。例如,如果我们知道一个函数f(x) = x^2的反函数是g(y) = (1/2y)^2,那么我们可以直接对g(y)求导得到其导数为g(y) = y(1/2y^2 - 1/2)。
(sinx)=cosx,即正弦的导数是余弦。(cosx)=-sinx,即余弦的导数是正弦的相反数。(tanx)=(secx)^2,即正切的导数是正割的平方。(cotx)=-(cscx)^2,即余切的导数是余割平方的相反数。(secx)=secxtanx,即正割的导数是正割和正切的积。
链式法则:链式法则是求导的基本方法之一,它可以用于求解复合函数的导数。对于反函数求导,我们可以将原函数与反函数看作是一个复合函数,然后利用链式法则进行求解。具体步骤如下:首先求出原函数的导数,然后将原函数的导数与反函数的导数相乘,最后将结果除以原函数的值。
同理可以求其他几个反三角函数的导数。所以以后在求涉及到反函数的导数时,先将反函数求出来,只是这里的反函数是以x为因变量,y为自变量,这个要和我们平时的区分开。最后将y想法设法换成x即可。
反三角函数运算公式
1、也没什么,就是三角函数的反函数 就几个常用的记住就好了,arcsinπ/6=π/...。。
2、余割为x的角。三角函数的反函数是个多值函数,因为它并不满足一个自变量对应一个函数值的要求,其图像与其原函数关于函数 y=x 对称。欧拉提出反三角函数的概念,并且首先使用了“arc+函数名”的形式表示反三角函数。关于反三角函数的计算公式比较多。
3、反三角函数是一类与基本三角函数互为逆运算的函数,它们之间的关系可以通过以下公式来表示: cos(反余弦x) = √(1 - x^2),这意味着当知道一个角的余弦值时,可以反向计算出对应的角度。 反正弦(-x) = -反正弦x,这表明正弦值的符号变化会导致角度取相反的值。
4、sin(arcsinx)=x 计算过程如下:设y=arcsinx 然后得出:x=sin(y)于是可得:sin(arcsinx)=sin(y)最后得出:sin(arcsinx)=x 反三角函数 具体来说,它们是正弦,余弦,正切,余切,正割和辅助函数的反函数,并且用于从任何一个角度的三角比获得一个角度。
5、反三角函数计算公式大全如下:arcsin(-x)=-arccosx。arccos(-x)=π-arccosx。arctan(-x)=-arctanx。arccot(-x)=π-arccotx。arcsinx+arccosx=π/2=arctanx+arccotx。反三角函数是一种基本初等函数。
6、反三角函数包含12个基本公式,其中一些较为基础的公式包括: 对于任意x,arcsin(-x)等于-arcsinx。 对于任意x,arctan(-x)等于-arctanx。 对于任意x,arccot(-x)等于π-arccotx。
基本反函数公式16个
反余割函数:余割函数y=cscx在[-π/2,0)U(0,π/2]上的反函数,叫做反余割函数。记作arccscx,表示个余割值为x的角,该角的范围在[π/2,0)U(0,π/2]区间内。
反三角函数公式包括arcsin(-x)=-arcsinx。arccos(-x)=π-arccosx。arctan(-x)=-arctanx。arccot(-x)=π-arccotx。arcsinx+arccosx=π/2=arctanx+arccotx。sin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)。
(4) 用f(x)的值域确定f-1(x)的定义域。 我们知道,函数y=f(x)若存在反函数,则y=f(x)与它的反函数y=f-1(x)有如下性质: 性质 若y=f-1(x)是函数y=f(x)的反函数,则有f(a)=bf-1(b)=a。 这一性质的几何解释是y=f(x)与其反函数y=f-1(x)的图象关于直线y=x对称。
公式:∫x^9dx/(1+x^20)。反正弦函数的求导:(arcsinx)=1/√(1-x^2)。反余弦函数的求导:(arccosx)=-1/√(1-x^2)。反正切函数的求导:(arctanx)=1/(1+x^2)。反余切函数的求导:(arccotx)=-1/(1+x^2)。