立体几何证明定理
立体几何常用证明定理高中的: 平行线性质定理 该定理描述了平行线间的性质,如在同一平面内,两条平行线间的距离保持不变。这一定理是证明涉及平行线问题的基础。 相似三角形判定定理与性质定理 这些定理用于证明两个三角形是否相似,以及相似三角形对应的边和角之间的关系。
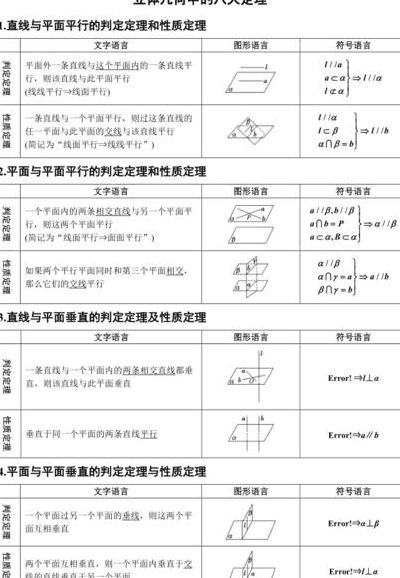
立体几何证明定理:线面平行的判定定理和性质定理;面面平行的判定定理和性质定理;线面垂直的判定定理和性质定理(或定义);面面垂直的判定定理和性质定理。立体几何证明主要考察空间中线与线、线与面、面与面的平行和垂直问题。
等角定理:如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等。
立体几何证明过程最常用到的定理
等角定理:如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等。
立体几何常用证明定理高中的: 平行线性质定理 该定理描述了平行线间的性质,如在同一平面内,两条平行线间的距离保持不变。这一定理是证明涉及平行线问题的基础。 相似三角形判定定理与性质定理 这些定理用于证明两个三角形是否相似,以及相似三角形对应的边和角之间的关系。
有六种:定义法。垂面法。射影定理。三垂线定理。向量法。转化法。
立体几何证明定理:线面平行的判定定理和性质定理;面面平行的判定定理和性质定理;线面垂直的判定定理和性质定理(或定义);面面垂直的判定定理和性质定理。立体几何证明主要考察空间中线与线、线与面、面与面的平行和垂直问题。
立体几何常用证明定理高中的。
立体几何常用证明定理高中的: 平行线性质定理 该定理描述了平行线间的性质,如在同一平面内,两条平行线间的距离保持不变。这一定理是证明涉及平行线问题的基础。 相似三角形判定定理与性质定理 这些定理用于证明两个三角形是否相似,以及相似三角形对应的边和角之间的关系。
直线与平面平行的判定定理:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行。直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
等角定理:如果一个角的两边和另一个角的两边分别平行,并且方向相同,那么这两个角相等。
判定定理 一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。性质定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行。(3)直线与平面垂直 判定定理 一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。性质定理 垂直于同一个平面的两条直线平行。
线面垂直的判定定理和性质定理(或定义);面面垂直的判定定理和性质定理。立体几何证明主要考察空间中线与线、线与面、面与面的平行和垂直问题。随机组合之后,就产生了6种问题形式:线线平行、线线垂直、线面平行、线面垂直、面面平行和面面垂直。
求立体几何8大定理
1、直线与平面平行的判定定理:如果平面外的一条直线与平面内的一条直线平行,则这条直线与平面平行。直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行。
2、立体几何八大定理:直线与平面平行的判定定理。直线与平面平行的性质定理。平面与平面平行的判定定理。平面与平面平行的性质定理。直线与平面垂直的判定定理。直线与平面垂直的性质定理。平面与平面垂直的判定定理。平面与平面垂直的性质定理。
3、如果两条直线同垂直于一个平面,那么这两条直线平行。
4、说明:b⊥L不一定成立。如图,设直线a对应AB,则直线b对应BF或者BE都可以满足条件。而直线L则是对应CD。由此可知b⊥L不一定成立。证明α垂直于β实际上就是定理“如果一个平面经过了另一个平面的一条垂线,那么这两个平面互相垂直”的证明。
5、直线与平面平行是几何学中基本的概念,涉及到空间中线与面的关系。判定定理指出,只要平面外一条直线与平面内一条直线平行,即可推断这条直线与整个平面平行。性质定理则说明,若直线与平面平行且两个平面相交,直线与交线必然平行。