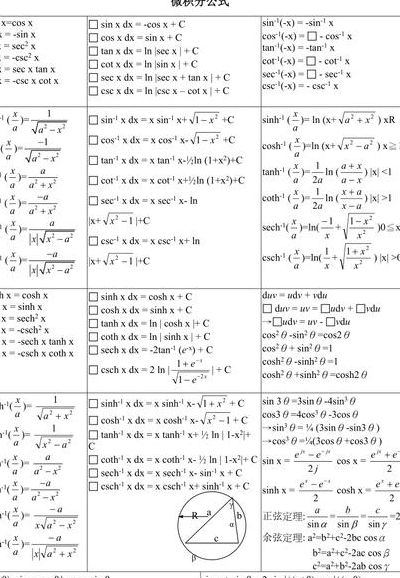
高数常用微积分公式24个
高数有24个基本积分公式:∫kdx=kx+C(k是常数)。∫xdx=+1+C,(≠1)+1dx。∫=ln|x|+Cx1。∫dx=arctanx+C21+x1。∫dx=arcsinx+C21x。∫cosxdx=sinx+C。∫sinxdx=cosx+C。∫sec∫csc2xdx=tanx+Cxdx=cotx+C2。∫secxtanxdx=secx+C。
令u=cos(x),则∫u du = sin(x) + C = u + C = cos(x) + C 以上是高数中的基本积分公式,它们是解决积分问题的重要工具。
微积分中常用的积分公式包括: 幂函数的积分公式:∫x^αdx = x^(α+1)/(α+1) + C,其中α ≠ -1。 倒数函数的积分公式:∫1/x dx = ln|x| + C。 指数函数的积分公式:∫a^x dx = a^x/lna + C,其中a 是常数。
微积分24个基本公式是什么?
基本积分表共24个公式:∫ kdx = kx + C (k是常数 ) x μ ∫ x dx = μ + 1 + C , ( μ ≠ ?1) μ +1dx ( 3) ∫ = ln | x | + C x1 ( 4) ∫ dx = arctan x + C 2 1+ x 1 。
常数倍积分公式:∫ kdx = kx + C 其中,k 是任意常数。 幂函数积分公式:∫ x^μ dx = μx^(μ+1)/(μ+1) + C 注意:当 μ ≠ -1 时适用。
微积分公式Dxsinx=cosxcosx=-sinxtanx=sec2xcotx=-csc2xsecx=secxtanxcscx=-cscxcotx。
以下是改写后的文章内容:求导是微积分中的基础概念,以下是24个基本求导公式,它们在理解和应用导数时起到关键作用: 常数的导数为零,即C = 0。 复合幂函数的导数遵循(x^n)= n * x^(n-1)。 三角函数的导数有(sin x)= cos x,(cos x)= -sin x。
基本导数公式是微积分中的基石,它们概括了各种常见函数的导数。以下是24个基本导数公式: 对于常数函数y=c,其导数y=0。 当函数为y=x^μ(μ为非零常数),其导数为y=μx^(μ-1)。
微积分常用公式有哪些
1、牛顿-莱布尼茨公式,又称为微积分基本公式;格林公式,把封闭的曲线积分化为区域内的二重积分,它是平面向量场散度的二重积分;高斯公式,把曲面积分化为区域内的三重积分,它是平面向量场散度的三重积分;斯托克斯公式,与旋度有关。
2、微积分中常用的积分公式包括: 幂函数的积分公式:∫x^αdx = x^(α+1)/(α+1) + C,其中α ≠ -1。 倒数函数的积分公式:∫1/x dx = ln|x| + C。 指数函数的积分公式:∫a^x dx = a^x/lna + C,其中a 是常数。
3、基本积分表共24个公式:∫ kdx = kx + C (k是常数 ) x μ ∫ x dx = μ + 1 + C , ( μ ≠ ?1) μ +1dx ( 3) ∫ = ln | x | + C x1 ( 4) ∫ dx = arctan x + C 2 1+ x 1 。
4、微积分常用公式包括:导数公式、积分公式、泰勒公式、洛必达法则等。导数公式: 常数函数的导数:对于任意常数c,其导数为0,即dc/dx = 0。 幂函数的导数:对于x^n(n为实数),其导数为nx^(n-1)。
5、牛顿-莱布尼茨公式,又称为微积分基本公式;格林公式,把封闭的曲线积分化为区域内的二重积分,它是平面向量场散度的二重积分;高斯公式,把曲面积分化为区域内的三重积分,它是平面向量场散度的三重积分;斯托克斯公式,与旋度有关。
6、微积分基本公式是数学中的重要工具,它们涉及导数和微分的计算。以下是一些基本的微积分公式: 对于常数C,其微分为0:d(C) = 0。 对于变量x的μ次幂,其微分为μx^(μ-1)dx:d(x^μ) = μx^(μ-1)dx。 对于ax,其中a是常数,其微分为axlnadx:d(ax) = axlnadx。
微积分十个重要公式
1、提高计算精度,尤其是在数值微分和逼近方法中。 泰勒展开在不等式证明: 通过近似替换和比较,辅助证明不等式成立。 泰勒展开的收敛性: 研究展开式随着项数增加,其与原函数的误差如何收敛。这些公式是泰勒理论的基石,掌握它们对于深入理解微积分和应用其方法解决实际问题至关重要。
2、微积分公式Dxsinx=cosxcosx=-sinxtanx=sec2xcotx=-csc2xsecx=secxtanxcscx=-cscxcotx。
3、此外,三角函数积分公式和反三角函数积分公式在处理涉及三角函数的积分问题时也非常重要。这些公式允许我们求解形如sin(x)dx或arctan(x)dx的积分,这些积分在物理学、工程学和其他领域的应用中经常出现。总的来说,微积分的13个基本公式是求解各种积分问题的关键工具。
4、微积分中的基本公式:牛顿-莱布尼兹公式:若函数f(x)在[a,b]上连续,且存在原函数F(x),则f(x)在[a,b]上可积,且 b(上限)∫a(下限)f(x)dx=F(b)-F(a) 。
5、基本积分表共24个公式:∫ kdx = kx + C (k是常数 ) x μ ∫ x dx = μ + 1 + C , ( μ ≠ ?1) μ +1dx ( 3) ∫ = ln | x | + C x1 ( 4) ∫ dx = arctan x + C 2 1+ x 1 。