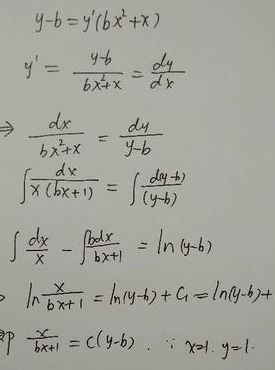微分方程。
1、微分方程的公式:一阶常微分方程通解 dydx+p(x)y=0dydx+p(x)y=0。齐次微分方程通解 y=ce∫p(x)dx。非齐次微分方程通解 y=e∫p(x)dx(c+∫q(x)e∫p(x)dxdx)。
2、微分方程公式:y+P(x)y=Q(x),微分方程,是指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。微分方程是伴随着微积分学一起发展起来的。
3、一般的、凡是表示未知函数、未知函数的导数与自变量之间的关系的方程,叫做微分方程。未知函数是一元函数的,叫常微分方程;未知函数是多元函数的、叫做偏微分方程。微分方程有时也简称方程。
4、(1)y=f(x),解法:直接积分。(2)y+py+q=f(x),解法:常数变易法、公式法。(3)y+py+qy=f(x),解法:特征方程法。(4)其他形式。
微分方程的一般形式有哪些?表达式是什么
1、微分方程的解通常是一个函数表达式y=f(x),(含一个或多个待定常数,由初始条件确定)。例如:其解为:其中C是待定常数;如果知道 则可推出C=1,而可知 y=-\cos x+1。
2、常微分方程通解公式是y=y(x)。隐式通解一般为f(x,y)=0的形式,定解条件,就是边界条件,或者初始条件 。 常微分方程,属数学概念。
3、一般的、凡是表示未知函数、未知函数的导数与自变量之间的关系的方程,叫做微分方程。未知函数是一元函数的,叫常微分方程;未知函数是多元函数的、叫做偏微分方程。微分方程有时也简称方程。
微分方程的通解公式
微分方程的通解公式:一阶常微分方程通解 dydx+p(x)y=0dydx+p(x)y=0。齐次微分方程通解 y=ce∫p(x)dx。非齐次微分方程通解 y=e∫p(x)dx(c+∫q(x)e∫p(x)dxdx)。
微分方程通解公式包括如下:对于一阶常微分方程,通解公式为:dy/dx=f(x)的通解dydx=f(x)dx。
常微分方程通解公式是:y=y(x)。隐式通解一般为f(x,y)=0的形式,定解条件,就是边界条件,或者初始条件 。 常微分方程,属数学概念。学过中学数学的人对于方程是比较熟悉的。
微分方程公式
1、微分方程公式:y+P(x)y=Q(x),微分方程,是指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。微分方程是伴随着微积分学一起发展起来的。
2、微分方程通解公式包括如下:对于一阶常微分方程,通解公式为:dy/dx=f(x)的通解dydx=f(x)dx。
3、常微分方程通解公式是:y=y(x)。隐式通解一般为f(x,y)=0的形式,定解条件,就是边界条件,或者初始条件 。 常微分方程,属数学概念。学过中学数学的人对于方程是比较熟悉的。