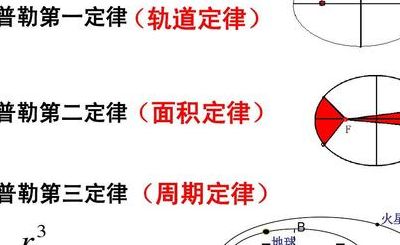
如何用动量守恒定律解释开普勒第二定律。。
开普勒第二定律:任一行星和太阳之间的联线,在相等的时间内扫过的面积相等,即掠面速度不变.利用角动量守恒定律证明如下。
矢径在相等的时间内扫过的面积相等,这就是开普勒行星运动三定律之一—开普勒第二定律 。角动量守恒也是微观物理学中的重要基本规律。
开普勒第二定律:太阳与任何一个行星的连线在相等的时间内扫过的面积相等。开普勒第三定律:行星绕太阳运行轨道半长轴r的立方与其公转周期T的二次方成正比。
自然界的三大守恒定律分别为质量守恒、能量守恒、电荷守恒定律 。
动量守恒定律二级结论是初态总动量等于末态总动量。首先根据牛顿运动第二定律F=mg,得F=m(v1-v2)t 所以Ft=mv1-mv2 也就是动量定律,合外力的冲量等于动量的改变量。
开普勒第二定律(面积定律):从太阳到行星所联接的直线在相等时间内扫过同等的面积。
什么是开普勒第二定律
1、面积定律是开普勒第二定律,从太阳到行星所联接的直线在相等时间内扫过同等的面积。用公式表示为:SAB=SCD=SEK。周期定律 周期定律是开普勒第三定律,所有的行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
2、开普勒第二定律:行星在轨道上的面积相等 开普勒第二定律也被称为面积速度定律或开普勒第二定律。根据这个定律,行星在相同时间内扫过的面积是相等的。
3、开普勒行星运动第二定律,也称面积定律,指的是太阳系中太阳和运动中的行星的连线(矢径)在相等的时间内扫过相等的面积。1该定律是德国天文学家约翰尼斯·开普勒发现的三条开普勒定律之一。
开普勒第二定律的介绍
1、开普勒行星三大定律为我们解释了行星运动的基本规律。第一定律揭示了行星轨道的椭圆性质;第二定律描述了行星在轨道上扫过的面积相等;第三定律则建立了行星轨道周期与半长轴的关系。
2、开普勒第二定律(面积定律):从太阳到行星所联接的直线在相等时间内扫过同等的面积。用公式表示为:SAB=SCD=SEK。这一定律实际揭示了行星绕太阳公转的角动量守恒。
3、开普勒行星运动第二定律,也称面积定律,指的是太阳系中太阳和运动中的行星的连线(矢径)在相等的时间内扫过相等的面积。1该定律是德国天文学家约翰尼斯·开普勒发现的三条开普勒定律之一。
4、面积定律是开普勒第二定律,从太阳到行星所联接的直线在相等时间内扫过同等的面积。用公式表示为:SAB=SCD=SEK。周期定律 周期定律是开普勒第三定律,所有的行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
如何证明开普勒第二定律?
同时,极坐标形式下,面积元为:dS=(1/2)(r^2)dθ,代入上面的求得的r,可以得到:dS=L/(2mw)dθ。又w=dθ/dt,即:dS=L/(2m)dt。得到了开普勒第二定律。
开普勒第二定律的证明介绍如下:根据角动量守恒定律,行星绕恒星运动的轨道都是椭圆,且恒星处在椭圆的某个焦点上。极坐标形式下,面积元为dS=(1/2)(r^2)dθ。
开普勒第一定律(椭圆定律):每一行星沿一个椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点中。开普勒第二定律(面积定律):从太阳到行星所联接的直线在相等时间内扫过同等的面积。
开普勒第一定律和第二定律是什么?
轨道定律 轨道定律是开普勒第一定律,每一行星沿一个椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点中。面积定律 面积定律是开普勒第二定律,从太阳到行星所联接的直线在相等时间内扫过同等的面积。
开普勒第二定律(面积定律):从太阳到行星所联接的直线在相等时间内扫过同等的面积。用公式表示为:SAB=SCD=SEK。这一定律实际揭示了行星绕太阳公转的角动量守恒。
开普勒第一定律(轨道定律):每一行星沿一个椭圆轨道环绕太阳,而太阳则处在椭圆的一个焦点中。开普勒第二定律(面积定律):从太阳到行星所联接的直线在相等时间内扫过同等的面积。用公式表示为:SAB=SCD=SEK。
开普勒第二定律公式
1、开普勒第二定律公式:Sek=Scd=Sab。开普勒行星运动第二定律,也称等面积定律,指的是太阳系中太阳和运动中的行星的连线(矢径)在相等的时间内扫过相等的面积。
2、开普勒第二定律(面积定律):从太阳到行星所联接的直线在相等时间内扫过同等的面积。用公式表示为:SAB=SCD=SEK。开普勒第三定律(周期定律):所有的行星的轨道的半长轴的三次方跟公转周期的二次方的比值都相等。
3、开普勒第二定律(面积定律):从太阳到行星所联接的直线在相等时间内扫过同等的面积。用公式表示为:SAB=SCD=SEK。这一定律实际揭示了行星绕太阳公转的角动量守恒。